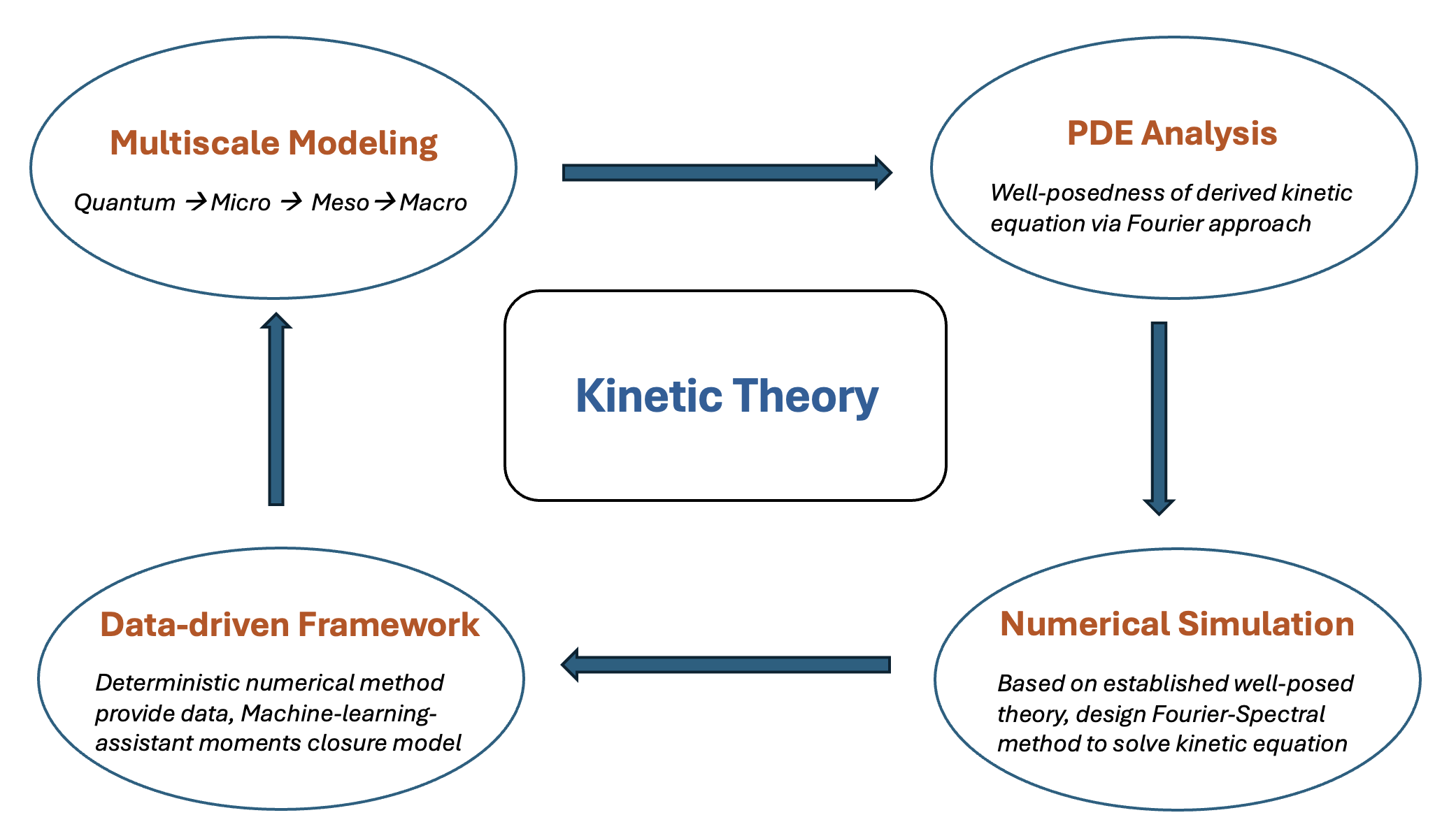
Research

My current research interests and expertise lie in developing multiscale, analytical, computational, and data-driven methods for the kinetic theory, mainly the Boltzmann equation and related kinetic models, arising from statistical physics, fluid dynamics, material science, biology, and so forth. Specifically,

• (I) Multiscale Modeling: Kinetic limit of many-particle dynamical complex systems, hydrodynamic limit of kinetic models, and semi-classical limit of quantum systems;
• (II) Theoretical Analysis for Kinetic PDE: Well-posedness and asymptotic behavior of Boltzmann equation and its related models via Fourier approach;
• (III) Numerical Simulation for Kinetic PDE: Fourier-Spectral method and the fast algorithm for kinetic equation with stability/convergence analysis;
• (IV) Data-driven and Machine-Learning-assisted Methods in Kinetic Theory: Data assimilation, Uncertainty Quantification (UQ) and machine-learning moments closure model.

(I) From multiscale modeling perspective: In the classical hierarchy of fluid mechanics, the kinetic equation serves as the bridge that connects many-particle dynamical systems on the microscopic scale to the fluid system on the macroscopic level. 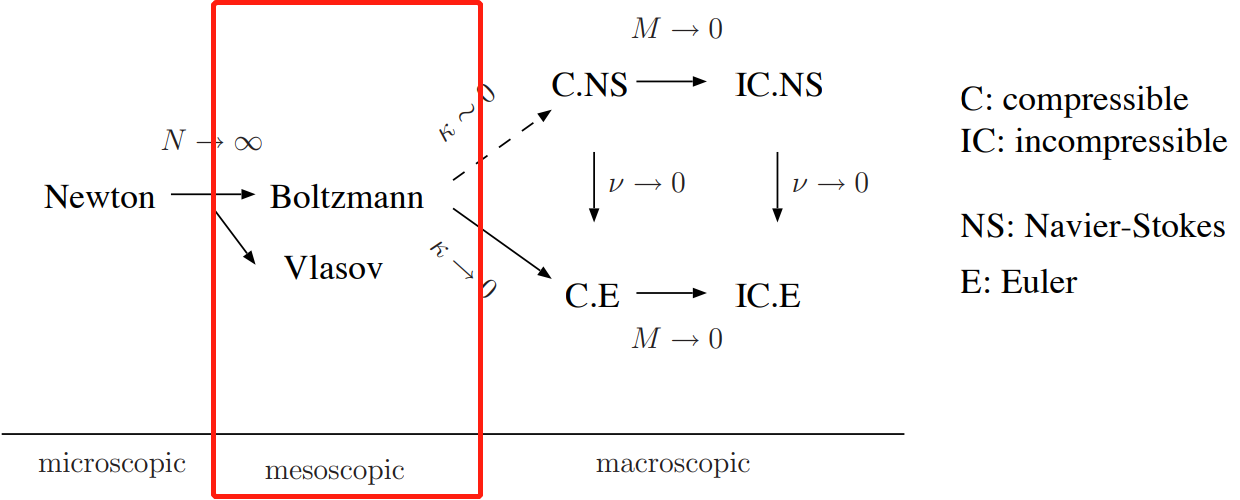Recently, we mainly focus on the multiscale modeling derivation concerning:

• Objective Molecular Dynamics (OMD), leveraging the symmetry and invariance of atomic forces and significantly reducing the computational cost compared to conventional Molecular Dynamics.
• Fluid-particle two-phase coupled system such as Vlasov-Fokker-Planck equation coupled with Navier-Stokes equations, and Boltzmann equation of (multi-species) gas mixture.

• Semi-classical limit for the Schrodinger equation and the effective dynamics of 2D material graphene.
  

  Corresponding Papers:
  [1] R. D. James, K. Qi and L. Wang, On the kinetic description of the objective molecular dynamics, SIAM Multiscale Model. Simul., 2024. (Link).
  [2] K. Qi, L. Wang and A. B. Watson Radiative transport in a periodic structure with band crossings, SIAM J. Appl. Math., 2024. (Link).
  [3] Z. Fang, K. Qi and H. Wen, The small Deborah number limit for the fluid-particle flows I: incompressible case, Math. Models Methods Appl. Sci.(M3AS), 12(34), 2024. (Link).
  [4] Z. Fang, K. Qi and H. Wen, The small Deborah number limit for the fluid-particle flows II: compressible case, preprint, 2024.
  [5] Z. Fang and K. Qi, From the Boltzmann equation for gas mixture to the two-fluid incompressible hydrodynamic system, preprint, 2024. (Link).

(II) From theoretical perspective: I mainly focus on the Measure-valued solutions to the Boltzmann equation and its variants (such as the inelastic collision model, homo-energetic model, etc.), including the existence, uniqueness, self-similar type asymptotic behavior and, so forth. The heuristic motivations that push me to look for Measure-valued solutions include:

• Since the solution to the Boltzmann equation itself represents a probability distribution function in phase space, it is natural to find solutions in the probability measure space.
• The Fourier Transform provides a powerful tool from which the Bobylev Identity (A. Bobylev 1988) comes, and a new classification (Y. Morimoto, S. Wang and T. Yang 2015) on characteristic functions has been carefully constructed and studied.

• In contrast with other perturbation frameworks, albeit with some limitations, the measure-valued solution theory has the potential to be applied for more general initial conditions.

  Corresponding Papers:
  [1] K. Qi, On the Measure Valued Solution to the Inelastic Boltzmann Equation with Soft Potentials, J. Stat. Phys., 183, 27, 2021. (Link).
  [2] K. Qi, Measure valued solution to the Spatially Homogeneous Boltzmann Equation with Inelastic Long-Range Interactions, J. Math. Phys., 63(2), 021503, 2022. (Link).
  [3] J. W. Jang and K. Qi, Global existence and moment creation for the inelastic Boltzmann equation for hard potentials without angular cutoff, preprint, 2023. (Link).
  [4] J. W. Jang and K. Qi, Measure-valued solution to the inelastic Boltzmann equation for hard potentials without angular cutoff, Proceedings of RGD32, AIP Conf. Proc., 2996, 040008, 2024. (Link).

(III) From numerical perspective, I mainly focus on developing an efficient and accurate numerical method for solving kinetic equations, i.e., the Fast Fourier-Spectral Method (I. Gamba, J. Haack, C. Hauck and J. Hu 2017). Compared with other stochastic methods (e.g., DSMC) or deterministic methods (e.g., Discrete Velocity Models), it has the following advantages: -Transform the high dimensional and nonlinear integral operator, the main trouble-maker in solving the Boltzmann equation, into a relatively simple weighted convolutional structure.

• Provide significantly more accurate results with less numerical complexity O(N^6) and storage requirement O(MN^4, M<N), and utilize FFT to achieve further acceleration and reduce the computational cost to (MN^3logN, M<N).

• Serve as a “black-box” solver to be combined with other time and spatial discretization methods to simulate the more practical complete Boltzmann equation. 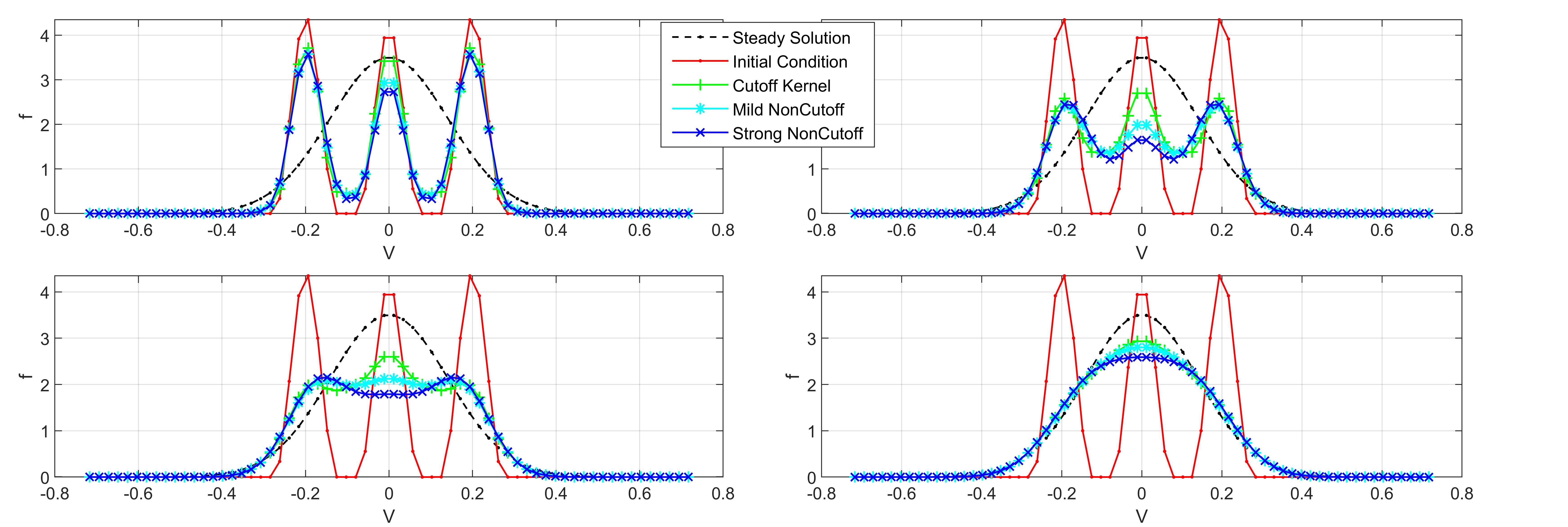Besides, I’m also working on rigorous proof of the consistency and stability of the Fourier-Spectral Method for both cutoff and non-cutoff cases. Considering some intrinsic drawbacks of the Spectral method, which, e.g., only preserves mass conservation but fails in the momentum and energy conservation law (though still preserved up to spectral accuracy), some refined approaches are under investigation.

  Corresponding Papers:
  [1] J. Hu and K. Qi, A fast Fourier spectral method for the homogeneous Boltzmann equation with non-cutoff collision kernels, J. Comput. Phys., 423:109806, 2020. (Link).
  [2] J. Hu, K. Qi and T. Yang, A new stability and convergence proof of the Fourier-Galerkin spectral method for the spatially homogeneous Boltzmann equation, SIAM J. Numer. Anal., 59(2), 613-633, 2021. (Link).
  [3] R. D. James, K. Qi and L. Wang, An anisotropic rescaling velocity method for the homo-energetic Boltzmann equation, in preparation, 2024.

(IV) From data-driven and machine-learning-assisted perspective: With the explosion of available data and the advancements of machine-learning techniques, we aim to leverage Data-driven methodologies to enhance our research in kinetic theory and related multiscale models. Rather than directly applying Machine-Learning tools to solve equations, we envision them providing heuristic and practical support in the modeling process, particularly in addressing the moments closure problem of kinetic-type equations.

• Generate benchmark/training data with Uncertainty Quantification (UQ).
• Collect unmeasurable/sufficient data via Data Assimilation.

• Apply obtained data to derive the moments closure models by Machine-Learning-assisted techniques.

  Corresponding Papers:
  [1] L. Liu and K. Qi, Convergence of the Fourier-Galerkin spectral method for the Boltzmann equation with uncertainties, Commun. Math. Sci., 22(7), 1897-1925, 2024. (Link).
  [2] L. Liu and K. Qi, Spectral convergence of a semi-discretized numerical system for the spatially homogeneous Boltzmann equation with uncertainties, SIAM/ASA J. Uncertain. Quantif., 12(3), 812-841 2024. (Link).
  [3] J. Lu, K. Qi, L. Wang and J. Calder, Recovering the data of unclosed hydrodynamics from partial observations, preprint, 2024. (Link).
  [4] J. W. Jang, J. Y. Lee, L. Liu, K. Qi and Z. Zhu, Machine-learning moments closure model for the multi-phase computations of the semiclassical limit of the Schrodinger equation, in preparation, 2024.
  [5] J. Huang, L. Liu, K. Qi and J. Wan, On the machine-learning moments closure for the linear semiconductor Boltzmann equation, in preparation, 2024.